Introduction

We discuss the problem of density of compactly supported smooth functions in the fractional Sobolev space \(W^{s,p}(\Omega )\), which is well known to hold when \(\Omega\) is a bounded Lipschitz domain and \(sp\le 1\) [14, Theorem 1.4.2.4],[26, Theorem 3.4.3]. We extend this result to bounded, plump open sets with a dimension of the boundary satisfying certain inequalities. To this end, we use the Assouad dimensions and codimensions. We also describe explicitly the closure of \(C_{c}^{\infty }(\Omega )\) in the fractional Sobolev space, provided that \(\Omega\) satisfies the fractional Hardy inequality.

Let \(\Omega \subset \mathbb {R}^{d}\) be an open set. Let \(0<s<1\) and \(1\le p<\infty\). We recall that the fractional Sobolev space is defined as

$$\begin{aligned} W^{s,p}(\Omega )=\left\{ f\in L^{p}(\Omega ):\int _{\Omega }\int _{\Omega }\frac{|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx<\infty \right\} . \end{aligned}$$

This is a Banach space endowed with the norm

$$\begin{aligned} \Vert f\Vert _{W^{s,p}(\Omega )}=\Vert f\Vert _{L^{p}(\Omega )}+[f]_{W^{s,p}(\Omega )}, \end{aligned}$$

where \([f]_{W^{s,p}(\Omega )}=\left( \int _{\Omega }\int _{\Omega }\frac{|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\right) ^{1/p}\) is called the Gagliardo seminorm. Throughout the paper we consider only real-valued functions, but we note that all results are clearly valid also for complex-valued functions, by means of decomposing them into a sum of real and imaginary part.

Definition 1

By \(W_{0}^{s,p}(\Omega )\)we denote the closure of \(C_{c}^{\infty }(\Omega )\) (the space of all smooth functions with compact support in\(\Omega\)) in \(W^{s,p}(\Omega )\) with respect to the Sobolev norm.

The following theorem is our main result on the connection between \(W_{0}^{s,p}(\Omega )\) and \(W^{s,p}(\Omega )\). For the relevant geometric definitions, we refer the Reader to Sect. 2. Here we only note that for bounded Lipschitz domains one has \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega ) = {{\,\mathrm{\overline{co\,dim}}\,}}_{A}(\partial \Omega ) = 1\) and the other geometrical assumptions of Theorem 2 do hold (that is, bounded Lipschitz domains are \((d-1)\)-homogeneous and \(\kappa\)-plump), hence the classical case is included.

Theorem 2

Let \(\Omega \subset \mathbb {R}^d\) be a nonempty bounded open set, let \(0<s<1\) and \(1\le p <\infty\).

  1. (I)

    If \(sp<{{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )\), then \(W_{0}^{s,p}(\Omega )=W^{s,p}(\Omega )\).

  2. (II)

    If \(\Omega\) is a \((d-sp)\)-homogeneous set, \(sp={{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )\) and \(p>1\), then \(W_{0}^{s,p}(\Omega )=W^{s,p}(\Omega )\).

  3. (III)

    If \(\Omega\) is \(\kappa\)-plump and \(sp>{{\,\mathrm{\overline{co\,dim}}\,}}_{A}(\partial \Omega )\), then \(W_{0}^{s,p}(\Omega )\ne W^{s,p}(\Omega )\).

We remark that a result similar to the part (I) and (III) in the Theorem 2 was obtained by Caetano in [6] in the context of Besov spaces and Triebel–Lizorkin spaces, but with the Minkowski dimension instead of Assouad dimension. That result is not directly comparable with ours, as for less regular domains spaces \(W^{s,p}\) do not necessarily coincide with the appropriate Triebel–Lizorkin spaces. We refer the Reader to [5] for a discussion on the space \(W^{s,p}_0\) and different similarly defined spaces. We also want to mention that analogous, but slightly different problems were considered in [12] (spaces of functions vanishing outside \(\Omega\)), [8] (the weighted case) and [1] (spaces with variable exponents).

In the case (III) above, we also obtain the following characterization of the space \(W_{0}^{s,p}(\Omega )\). For the proof, see Sect. 5.

Theorem 3

Let \(0<s<1\) and \(1\le p < \infty\). Suppose that \(\Omega \ne \emptyset\) is a bounded, open \(\kappa\)-plump set. If \({{\,\mathrm{\overline{co\,dim}}\,}}_{A}(\partial \Omega )<sp\), then

$$\begin{aligned} W_{0}^{s,p}(\Omega ) = \left\{ f\in W^{s,p}(\Omega ):\int _{\Omega }\frac{|f(x)|^{p}}{{{\,\mathrm{dist}\,}}(x,\partial \Omega )^{sp}}\,dx<\infty \right\} . \end{aligned}$$

(1)

In the case (I) of Theorem 2 equality (1) also holds, or in other words, we have an inclusion between the Sobolev and weighted \(L^p\) space, \(W^{s,p}(\Omega ) \subset L^p(\Omega , {{\,\mathrm{dist}\,}}(x,\partial \Omega )^{-sp})\). This fact is made quantitative in the next theorem; for its proof, see Sect. 5 as well.

Theorem 4

Let \(0<s<1\) and \(1\le p < \infty\). Suppose that \(\Omega \ne \emptyset\) is a bounded, open \(\kappa\)-plump set. If \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )>sp\), then there exists a constant c such that

$$\begin{aligned} \int _{\Omega }\frac{|f(x)|^{p}}{{{\,\mathrm{dist}\,}}(x,\partial \Omega )^{sp}}\,dx \le c \Vert f\Vert _{W^{s,p}(\Omega )}^p < \infty , \quad \text {for all}\; f\in W^{s,p}(\Omega ). \end{aligned}$$

(2)

Theorem 3 and 4 have classical (non-fractional) counterparts, see [20, Example 9.11] or [19].

Finally, we extend the results of [11, Theorem 1, Corollary 3]. Namely, we prove the case (T') in the following version of the fractional Hardy inequality. For the definitions of the conditions \({{\,\mathrm{WLSC}\,}}\) and \({{\,\mathrm{WUSC}\,}}\) , we refer the reader to the Appendix, while the plumpness and Assouad dimensions are defined in Sect. 2. We would also like to note that a special case of (T') (assuming in particular \(p=2\)) was proved in [25, Lemma 3.32] and [7].

Theorem 5

([11] in cases (T) and (F)) Let \(0<p<\infty\), \(H\in (0,1]\) and \(\eta \in \mathbb {R}\). Suppose \(\Omega \not =\emptyset\) is a proper \(\kappa\)-plump open set in \(\mathbb {R}^d\) and \(\phi :(0,\infty )\rightarrow (0,\infty )\) is a function so that either condition (T), or condition (T'), or condition (F) holds

(T):

\(\eta + \overline{\mathrm {dim}}_A(\partial \Omega ) - d<0\), \(\Omega\) is unbounded, \(\phi \in {{\,\mathrm{WUSC}\,}}(\eta ,0,H^{-1})\),

(T'):

\(\eta + \overline{\mathrm {dim}}_A(\partial \Omega ) - d<0\), \(\Omega\) is bounded, \(\phi \in {{\,\mathrm{WUSC}\,}}(\eta ,0,H^{-1})\),

(F):

\(\eta + \underline{\mathrm {dim}}_A(\partial \Omega ) - d > 0\), \(\Omega\) is bounded or \(\partial \Omega\) is unbounded, and \(\phi \in {{\,\mathrm{WLSC}\,}}(\eta ,0,H)\).

Then there exist constants \(c=c(d,s,p,\Omega ,\phi )\) and R such that the following inequality

$$\begin{aligned} \int _\Omega \frac{|u(x)|^p}{\phi (d_{\Omega }(x))}\,dx \le c \int _\Omega \!\int _{\Omega \cap B(x,Rd_{\Omega }(x))} \frac{|u(x)-u(y)|^p}{\phi (d_{\Omega }(x))d_{\Omega }(x)^d}\,dy\,dx\, + c\xi \Vert u\Vert _{L^p(\Omega )}^p, \end{aligned}$$

(3)

holds for all measurable functions u for which the left hand side is finite, with \(\xi =0\) in the cases (T) and (F) and \(\xi =1\) in the case \((T')\).

There is a huge literature about fractional Hardy inequalities; we refer the Reader to [9, 11, 17] and the references therein. We would also like to draw Reader's attention to a paper [23] from 1999 by Farman Mamedov. This not very well-known paper is one of the first to deal with multidimensional fractional order Hardy inequalities.

The authors would like to thank Lorenzo Brasco for helpful discussions on the subject, in particular for providing a part of the proof of Theorem 2, and the anonymous referee for numerous comments which led to an improvement of the manuscript.

Geometrical definitions

We denote the distance from \(x\in \mathbb {R}^d\) to a set \(E\subset \mathbb {R}^d\) by \({{\,\mathrm{dist}\,}}(x,E)=\displaystyle \inf _{y\in E}|x-y|\); for open sets \(\Omega \subset \mathbb {R}^d\) we write \(d_{\Omega }(x)=\text {dist}(x,\partial \Omega )\).

Definition 6

Let \(r>0\). For open sets \(\Omega \subset \mathbb {R}^d\) , we define the inner tubular neighbourhood of \(\Omega\) as

$$\begin{aligned} \Omega _{r}=\left\{ x\in \Omega :d_{\Omega }(x)\le r\right\} , \end{aligned}$$

and for arbitrary sets \(E\subset \mathbb {R}^d\) , we define the tubular neighbourhood of E as

$$\begin{aligned} \widetilde{E}_{r}=\left\{ x\in \mathbb {R}^{d}: {{\,\mathrm{dist}\,}}(x, E) \le r\right\} . \end{aligned}$$

Definition 7

[18, Section 3] Let \(E\subset \mathbb {R}^{d}\). The lower Assouad codimension \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(E)\) is defined as the supremum of all \(q\ge 0\), for which there exists a constant \(C=C(q)\ge 1\) such that for all \(x\in E\) and \(0<r<R<{{\,\mathrm{diam}\,}}E\) , it holds

$$\begin{aligned} \left| \widetilde{E}_{r}\cap B(x,R)\right| \le C\left| B(x,R)\right| \left( \frac{r}{R}\right) ^{q}. \end{aligned}$$

Conversely, the upper Assouad codimension \({{\,\mathrm{\overline{co\,dim}}\,}}_{A}(E)\) is defined as the infimum of all \(s\ge 0\), for which there exists a constant \(c=c(s)>0\) such that for all \(x\in E\) and \(0<r<R<{{\,\mathrm{diam}\,}}E\) , it holds

$$\begin{aligned} \left| \widetilde{E}_{r}\cap B(x,R)\right| \ge c\left| B(x,R)\right| \left( \frac{r}{R}\right) ^{s}. \end{aligned}$$

We remark that having strict inequality \(R<{{\,\mathrm{diam}\,}}E\) above makes the definitions applicable also for unbounded sets E; for bounded sets E we could have \(R\le {{\,\mathrm{diam}\,}}E\).

In Euclidean space \(\mathbb {R}^{d}\) , we have \(\underline{\text {dim}}_{A}(E)=d-{{\,\mathrm{\overline{co\,dim}}\,}}_{A}(E)\), \(\overline{\text {dim}}_{A}(E)=d-{{\,\mathrm{\underline{co\,dim}}\,}}_{A}(E)\), where \(\underline{\text {dim}}_{A}(E)\) and \(\overline{\text {dim}}_{A}(E)\) denote, respectively, the well known lower and upper Assouad dimension – see for example [18, Section 2] for this result. Recall that the upper Assouad dimension of a given set E is defined as the infimum of all exponents \(s\ge 0\) for which there exists a constant \(C=C(s)\ge 1\) such that for all \(x\in E\) and \(0<r<R<{{\,\mathrm{diam}\,}}E\) the ball \(B(x,R)\cap E\) can be covered by at most \(C(R/r)^s\) balls with radius r, centered at E. Analogously, the lower Assouad dimension is characterized by the supremum of all exponents \(t\ge 0\) for which there is a constant \(c=c(t)>0\) such that the ball \(B(x,R)\cap E\) can be covered by at least c\((R/r)^t\) balls with radius r and centered at E. If \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(E)={{\,\mathrm{\overline{co\,dim}}\,}}_{A}(E),\) we simply denote it by \({{\,\mathrm{co\,dim}\,}}_{A}(E)\).

We recall a geometric notion from [27].

Definition 8

A set \(E\subset \mathbb {R}^d\) is \(\kappa\) -plump with \(\kappa \in (0,1)\) if, for each \(0<r< {{\,\mathrm{diam}\,}}(E)\) and each \(x\in \overline{E}\), there is \(z\in \overline{B}(x,r)\) such that \(B(z,\kappa r)\subset E\).

Following [22, Theorem A.12], we define a notion of \(\sigma\)-homogenity.

Definition 9

Let \(E\subset \mathbb {R}^d\) and let \(V(E,x,\lambda ,r)=\{y\in \mathbb {R}^d:{{\,\mathrm{dist}\,}}(y,E)\le r, |x-y|\le \lambda r\}\). We say that E is \(\sigma\)-homogeneous, if there exists a constant L such that

$$\begin{aligned} |V(E,x,\lambda ,r)|\le Lr^{d}\lambda ^{\sigma } \end{aligned}$$

for all \(x\in E\), \(\lambda \ge 1\) and \(r>0\).

If \(0<r<R<{{\,\mathrm{diam}\,}}(E)\), then taking \(\lambda =R/r\) in the definition gives

$$\begin{aligned} \left| \widetilde{E}_{r} \cap B(x,R)\right| = \left| V\Big (E,x,\frac{R}{r},r\Big )\right| \le C\left| B(x,R)\right| \left( \frac{r}{R}\right) ^{d-\sigma }, \end{aligned}$$

where \(C=C(d,E)\) is a constant. This means that if \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(E)=s\), then \((d-s)\)-homogeneous sets are precisely these sets E, for which the supremum in the definition of the lower Assouad codimension is attained. For the definition of the concept of homogenity from a different point of view, the Reader may also see [22, Definition 3.2].

Finally, let us note that for example in part I of Theorem 2, we need the assumption \(sp<{{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )\) only to obtain the bound (5). For that a slightly weaker assumption in terms of Minkowski (co)dimension would suffice, however, we need Assouad (co)dimensions for other parts of the paper, and therefore, we prefer to use only them. Let us only recall that the upper Minkowski dimension of a set \(E\subset \mathbb {R}^d\) is defined as

$$\begin{aligned} \overline{\text {dim}}_{M}(E)=\inf \{s\ge 0: \limsup _{r\rightarrow 0}\left| \widetilde{E}_{r}\right| r^{d-s}=0\}, \end{aligned}$$

see for example [15, Section 2]. The statement of the part (I) of Theorem 2 remains true if we assume that \(sp<d-\overline{\text {dim}}_{M}(\partial \Omega )\).

Lemmas

The following lemma is the key to our further computations. We recall that \(\Omega _{\frac{3}{n}}\) appearing in (4) is the inner tubular neighbourhood of \(\Omega\), see Definition 6.

Lemma 10

Let

$$v_{n} (x) = \max \left\{ {\min \left\{ {2 - nd_{\Omega } (x),1} \right\},0} \right\} = \left\{ {\begin{array}{*{20}l} 1 \hfill &{{\text{when}}\;d_{\Omega } (x) \le 1/n,} \hfill & {} \hfill \\ {2 - nd_{\Omega } (x)} \hfill & {{\text{when}}\;1/n} < {d_{\Omega } (x) \le 2/n,} \hfill \\ 0 \hfill & {{\text{when}}\;d_{\Omega } (x)} > {2/n.} \hfill \\ \end{array} } \right.$$

There exists a constant \(C=C(d,s,p,\Omega )>0\) such that the following inequality holds for all functions \(f\in W^{s,p}(\Omega )\)

$$\begin{aligned}{}[fv_{n}]^{p}_{W^{s,p}(\Omega )} \le Cn^{sp}\int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx+C\int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx. \end{aligned}$$

(4)

Proof

Fix \(f\in W^{s,p}(\Omega )\) and define \(f_{n}=fv_{n}\). We have

$$\begin{aligned}{}[f_{n}]^{p}_{W^{s,p}(\Omega )}&=\int _{\Omega }\int _{\Omega }\frac{|f(x)v_{n}(x)-f(y)v_{n}(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&=\int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)v_{n}(x)-f(y)v_{n}(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\quad+2\int _{\Omega _{\frac{2}{n}}}\int _{\Omega \setminus \Omega _{\frac{3}{n}}}\frac{|f(x)v_{n}(x)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&=:J_{1}+2J_{2}. \end{aligned}$$

First we estimate \(J_{1}\),

$$\begin{aligned} 2^{1-p}J_{1}&\le \int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)|^{p}|v_{n}(x)-v_{n}(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\quad+\int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|v_{n}(y)|^{p}|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&=:K_{1}+K_{2}. \end{aligned}$$

Since \(|v_n|\le 1\), we obtain

$$\begin{aligned} K_{2}\le \int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx. \end{aligned}$$

Furthermore, \(|v_{n}(x)-v_{n}(y)|\le \min \{1,n|x-y|\}\), hence, for \(K_{1}\) we can compute that

$$\begin{aligned} K_{1}&\le \int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)|^{p}\left( \min \{1,n|x-y|\}\right) ^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\le \int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx\int _{|x-y|>1/n}\frac{\,dy}{|x-y|^{d+sp}}+n^{p}\int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx\int _{|x-y|<1/n}\frac{\,dy}{|x-y|^{d-(1-s)p}}\\&\le Cn^{sp}\int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx. \end{aligned}$$

Since \(|v_{n}|\le 1\), for \(J_{2}\) we have

$$\begin{aligned} J_{2}=&\int _{\Omega _{\frac{2}{n}}}\int _{\Omega \setminus \Omega _{\frac{3}{n}}}\frac{|f(x)|^{p}|v_{n}(x)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\le \int _{\Omega _{\frac{2}{n}}}|f(x)|^{p}\,dx\int _{\Omega \setminus \Omega _{\frac{3}{n}}}\frac{\,dy}{|x-y|^{d+sp}}\\&\le \int _{\Omega _{\frac{2}{n}}}|f(x)|^{p}\,dx\int _{B(x,1/n)^{c}}\frac{\,dy}{|x-y|^{d+sp}}\\&\le Cn^{sp}\int _{\Omega _{\frac{2}{n}}}|f(x)|^{p}\,dx. \end{aligned}$$

Hence, we obtain for some (new) constant C that

$$\begin{aligned}{}[f_{n}]^{p}_{W^{s,p}(\Omega )}&\le Cn^{sp}\int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx+C\int _{\Omega _{\frac{3}{n}}}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx. \end{aligned}$$

\(\square\)

Definition 11

By \(W_{c}^{s,p}(\Omega )\) , we denote the closure of all compactly supported functions in \(W^{s,p}(\Omega )\) (not necessarily smooth) with respect to the Sobolev norm.

The key property, which allows us to get rid of the smoothness and rely only on the compactness of the support, is the result below.

Proposition 12

We have \(W_{0}^{s,p}(\Omega )=W_{c}^{s,p}(\Omega )\).

Proof

This is a straightforward consequence of [10, Proposition 2 and proof of Theorem 8]. \(\square\)

It turns out that to prove the density of compactly supported functions in the fractional Sobolev space, we only need to find a sequence which approximates the function (the indicator of \(\Omega\)).

Lemma 13

Let \(\Omega\) be an open set such that \(|\Omega |<\infty\). We have

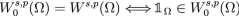
Proof

Implication "\(\implies\)" is obvious, therefore we proceed to prove the implication from right to left. According to Proposition 12, we need to prove that if the function 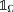can be approximated by some family of functions \(g_{n}\in W_{c}^{s,p}(\Omega )\), then every function \(f\in W^{s,p}(\Omega )\) can be approximated by functions from \(W_{c}^{s,p}(\Omega )\). Since \(L^{\infty }(\Omega )\cap W^{s,p}(\Omega )\) is dense in \(W^{s,p}(\Omega )\) (because the truncated functions \(f^{N}=\min \left\{ \max \left\{ f,-N\right\} ,N\right\}\) tend to f in \(W^{s,p}(\Omega )\), as \(N\longrightarrow \infty\)), we may assume that \(f\in L^{\infty }(\Omega )\). Moreover, we may also assume that \(0\le g_{n}\le 1\), because if in \(W^{s,p}(\Omega )\), then also , since we have \(|\widetilde{g}_{n}(x)-\widetilde{g}_{n}(y)|\le |g_{n}(x)-g_{n}(y)|\).

Define \(f_{n}=fg_{n}\in W_{c}^{s,p}(\Omega )\). Observe that

$$\begin{aligned}{}[f-f_{n}]^{p}_{W^{s,p}(\Omega )}&=\int _{\Omega }\int _{\Omega }\frac{|f(x)(1-g_{n}(x))-f(y)(1-g_{n}(y))|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\le 2^{p-1}\int _{\Omega }\int _{\Omega }\frac{|f(x)|^{p}|g_{n}(x)-g_{n}(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\quad+2^{p-1}\int _{\Omega }\int _{\Omega }\frac{|1-g_{n}(y)|^{p}|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\le 2^{p-1}\Vert f\Vert ^{p}_{\infty }[g_{n}]^{p}_{W^{s,p}(\Omega )}\\&\quad+2^{p-1}\int _{\Omega }\int _{\Omega }\frac{|1-g_{n}(y)|^{p}|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx. \end{aligned}$$

Since 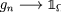in \(L^{p}(\Omega )\), there is a subsequence 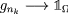almost everywhere. Hence, for such a subsequence we have

$$\begin{aligned}{}[f-f_{n_{k}}]^{p}_{W^{s,p}(\Omega )}&\le 2^{p-1}\Vert f\Vert ^{p}_{\infty }[g_{n_{k}}]^{p}_{W^{s,p}(\Omega )}\\&\quad+2^{p-1}\int _{\Omega }\int _{\Omega }\frac{|1-g_{n_{k}}(y)|^{p}|f(x)-f(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx. \end{aligned}$$

The first term above is convergent to 0, since in \(W^{s,p}(\Omega )\). The convergence of the second term follows from Lebesgue dominated convergence theorem. Moreover, it is trivial to show that \(f_{n}\longrightarrow f\) in \(L^{p}(\Omega )\) , and hence, the proof is finished. \(\square\)

Proof of Theorem 2

Proof of Theorem 2, case I

According to Lemma 13, we only need to prove that the function 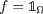can be approximated by compactly supported functions. Let \(f_{n}=fv_{n}\), where \(v_{n}\) is as in the Lemma 10 and let \(\underline{d}={{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )\). By Lemma 10 (note that in this case the second term in inequality (4) is 0), we have

$$\begin{aligned}{}[f_{n}]^{p}_{W^{s,p}(\Omega }\le Cn^{sp}\int _{\Omega _{\frac{3}{n}}}\,dx=Cn^{sp}\left| \Omega _{\frac{3}{n}}\right| . \end{aligned}$$

If \(sp<\underline{d}\), then, by the definition of lower Assouad codimension, for every \(\varepsilon >0\) we have

$$\begin{aligned} \left| \Omega _{\frac{3}{n}}\right| \le C'\left( \frac{1}{n}\right) ^{\underline{d}-\varepsilon }. \end{aligned}$$

(5)

Hence, for some new constant C we have

$$\begin{aligned}{}[f_{n}]^{p}_{W^{s,p}(\Omega )}\le Cn^{sp}n^{\varepsilon -\underline{d}}\longrightarrow 0, \end{aligned}$$

when \(n\longrightarrow \infty\), by choosing \(0<\varepsilon <\underline{d}-sp\), which is feasible thanks to our assumption. \(\square\)

Proof of Theorem 2, case II

We proceed like in the above proof of the first part of the Theorem 2 and obtain

$$\begin{aligned}{}[f_{n}]^{p}_{W^{s,p}(\Omega )}\le Cn^{sp}\left| \Omega _{\frac{3}{n}}\right| . \end{aligned}$$

Since \(\Omega\) is \((d-sp)\)-homogeneous and \({{\,\mathrm{\underline{co\,dim}}\,}}_{A}(\partial \Omega )=sp\), then it follows that \(\left| \Omega _{\frac{3}{n}}\right| \le C'n^{-sp}\) and, in consequence, the sequence \(\{f_{n}\}_{n\in \mathbb {N}}\) is bounded in \(W^{s,p}(\Omega )\).

The following argument was kindly pointed out to us by Lorenzo Brasco, see also [4, Theorem 4.4] for a similar argument. It is well known that for \(p>1\) the space \(W^{s,p}(\Omega )\) is reflexive. Hence, by Banach–Alaoglu and Eberlein–Šmulian theorem, there exists a subsequence \(\{f_{n_{k}}\}_{k\in \mathbb {N}}\) weakly convergent to some f. Since \(W_{0}^{s,p}(\Omega )\) is both closed and convex subset of \(W^{s,p}(\Omega )\), by [3, Theorem 2.3.6] it is also weakly closed, so we have \(f\in W_{0}^{s,p}(\Omega )\). Then it suffices to see that by the uniqueness of the limit, since \(f_{n_{k}}\) strongly converges to 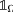in \(L^{p}(\Omega )\). This ends the proof. \(\square\)

Proof of Theorem 2, case III

Let \(\overline{d}={{\,\mathrm{\overline{co\,dim}}\,}}_{A}(\partial\Omega)\). We will show that the indicator of \(\Omega\) cannot be approximated by functions with compact support. Indeed, let \(u_{n}\) be any sequence of compactly supported functions such that 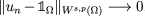In particular 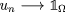in \(L^{p}(\Omega ),\) so there is a subsequence \(u_{n_{k}}\) convergent almost everywhere to . If \(sp>\overline{d}\), we can use the fractional Hardy inequality from [11, Corollary 3] in the case (F) with \(\beta =0\) to obtain

$$\begin{aligned}{}[u_{n_{k}}-]^{p}_{W^{s,p}(\Omega )}&=[u_{n_{k}}]^{p}_{W^{s,p}(\Omega )}=\int _{\Omega }\int _{\Omega }\frac{|u_{n_{k}}(x)-u_{n_{k}}(y)|^{p}}{|x-y|^{d+sp}}\,dy\,dx\\&\ge c\int _{\Omega }\frac{|u_{n_{k}}(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx. \end{aligned}$$

By Fatou's lemma,

$$\begin{aligned} 0=\lim _{k\rightarrow \infty }[u_{n_{k}}]^{p}_{W^{s,p}(\Omega )}&\ge c\int _{\Omega }\liminf _{k\rightarrow \infty }\frac{|u_{n_{k}}(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx\\&=c\int _{\Omega }\frac{\,dx}{d_{\Omega }(x)^{sp}}>0. \end{aligned}$$

We obtain a contradiction. \(\square\)

Example 14

(Lipschitz domains) Let \(\Omega\) be a bounded Lipschitz domain. In this case, we have \({{\,\mathrm{co\,dim}\,}}_{A}(\partial\Omega)=1\) and, by the cone property, \(\left| \Omega _{r}\right| =O(r)\), hence, Theorem 2 generalises the classical result [14, Theorem 1.4.2.4].

Example 15

(Koch snowflake) Let \(\Omega \subset \mathbb {R}^{2}\) denote the domain bounded by the Koch snowflake. It is well known that the Hausdorff dimension of the Koch curve is \(\frac{\log 4}{\log 3}\). Thus, also its Assouad dimension is \(\frac{\log 4}{\log 3}\), since it is a self-similar set satisfying open set condition, see [13, Corollary 2.11]. The Koch snowflake is a finite union of copies of Koch curves, therefore its Assouad dimension is again \(\frac{\log 4}{\log 3}\), see [13, Theorem 2.2] and [22, Theorem A.5(3)]. Hence \({{\,\mathrm{co\,dim}\,}}_{A}(\partial\Omega)=2-\frac{\log 4}{\log 3}\).

Moreover, by [21, Theorem 1.1] the volume of the inner tubular neighbourhood of \(\Omega\) is described by the formula

$$\begin{aligned} \left| \Omega _{r}\right| =G_{1}(r)r^{2-\frac{\log 4}{\log 3}}+G_{2}(r)r^{2}, \end{aligned}$$

where \(G_{1}\) and \(G_{2}\) are continuous, periodic functions (in consequence bounded). Hence, for \(r<1\) we have \(\left| \Omega _{r}\right| =O\left( r^{2-\frac{\log 4}{\log 3}}\right)\). Since in addition \(\Omega\) is \(\kappa\) - plump, by Theorem 2 we obtain that if \(p=1\), then \(C_{c}^{\infty }(\Omega )\) is dense in \(W^{s,p}(\Omega )\) if \(s< 2-\frac{\log 4}{\log 3}\) and is not dense if \(s> 2-\frac{\log 4}{\log 3}\). Moreover, if \(p>1\), then the density result holds if and only if \(sp\le 2-\frac{\log 4}{\log 3}\). We do not know what is happening in the remaining case \(p=1\) and \(s=2-\frac{\log 4}{\log 3}\).

The space \(W_{0}^{s,p}(\Omega )\)

Based on our previous results, we are able to describe explicitly the space \(W_{0}^{s,p}(\Omega )\) in some particular cases. Namely, we can describe this space for \(\Omega , s\) and p satisfying the following weak fractional Hardy inequality.

Definition 16

We say that \(\Omega\) admits a weak (s,p)–fractional Hardy inequality, if there exists a constant \(c=c(d,s,p,\Omega )\) such that for every \(f\in C_{c}^{\infty }(\Omega )\) it holds

$$\begin{aligned} \int _{\Omega }\frac{|f(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx\le c \Vert f\Vert _{W^{s,p}(\Omega )}^p. \end{aligned}$$

In the case when the norm \(\Vert f\Vert _{W^{s,p}(\Omega )}\) above can be replaced by the seminorm \([ f]_{W^{s,p}(\Omega )}\), we say that \(\Omega\) admits an (s,p)–fractional Hardy inequality.

Theorem 17

Suppose that \(\Omega\) admits a weak (s,p)-fractional Hardy inequality. Then

$$\begin{aligned} W_{0}^{s,p}(\Omega )=\left\{ f\in W^{s,p}(\Omega ):\int _{\Omega }\frac{|f(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx<\infty \right\} . \end{aligned}$$

Proof

By Lemma 10, if \(\int _{\Omega }\frac{|f(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx<\infty\), then \(f\in W_{0}^{s,p}(\Omega )\), because in this case

$$\begin{aligned} n^{sp}\int _{\Omega _{\frac{3}{n}}}|f(x)|^{p}\,dx\le 3^{sp}\int _{\Omega _{\frac{3}{n}}}\frac{|f(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx\longrightarrow 0, \end{aligned}$$

when \(n\longrightarrow \infty\). In fact, for that part we do not need the assumption about Hardy inequality.

Suppose that \(\Omega\) admits a weak (s,p)–Hardy inequality and \(f\in W_{0}^{s,p}(\Omega )\). Let \(f_{n}\) be a sequence of smooth and compactly supported functions convergent to f in \(W^{s,p}(\Omega ).\) In particular, \(f_{n}\longrightarrow f\) in \(L^{p}(\Omega )\), so there exists a subsequence \(f_{n_{k}}\) convergent to f almost everywhere. We have by Fatou lemma

$$\begin{aligned} \int _{\Omega }\frac{|f(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx&=\int _{\Omega }\lim _{k\rightarrow \infty }\frac{|f_{n_{k}}(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx\\&\le \liminf _{k\rightarrow \infty }\int _{\Omega }\frac{|f_{n_{k}}(x)|^{p}}{d_{\Omega }(x)^{sp}}\,dx\\&\le c\liminf _{k\rightarrow \infty }\Vert f_{n_{k}}\Vert ^{p}_{W^{s,p}(\Omega )}\\&=c\Vert f\Vert ^{p}_{W^{s,p}(\Omega )} < \infty . \end{aligned}$$

\(\square\)

Proof of Theorem 3

From part (F) of Theorem 5 with \(\eta =sp\), \(\varphi (t)=t^{sp}\), \(\Omega\) admits an (s,p)-fractional Hardy inequality and also a weak (s,p)-fractional Hardy inequality. Thus, the result follows from Theorem 17. \(\square\)

Proof of Theorem 4

From part (T') of Theorem 5, inequality (2) holds for all functions f for which the left hand side of (2) is finite. Thus by Theorem 3, it holds for all functions \(f\in W_{0}^{s,p}(\Omega )\). However, by part (I) of Theorem 2, \(W_{0}^{s,p}(\Omega ) = W^{s,p}(\Omega )\) , and the result follows. \(\square\)